Идеальный портфель для российского инвестора
Каким должен быть идеальный инвестиционный портфель? Над этим вопросом трудились много лет разные ученые. Особенно преуспел в этом вопросе американский экономист Гарри Марковиц. Он разработал методику формирования инвестиционного портфеля, направленную на оптимальный выбор активов, исходя из требуемого соотношения риска и доходности. Его идеи составляют основу современной портфельной теории.
Но в основном его труды основаны на статистике иностранных активов. В то время как российские инвесторы часто инвестируют не только в иностранные, но и в российские активы. Причем, доля отечественных активов часто превышает долю иностранных. Отдельно стоит заметить, что на доходность и риск иностранных активов очень заметно влияет курс рубля, который порой бывает очень волатильным. Поэтому западные исследования нам не очень помогут в поиске оптимального портфеля для российского инвестора.
Историческая доходность финансовых активов
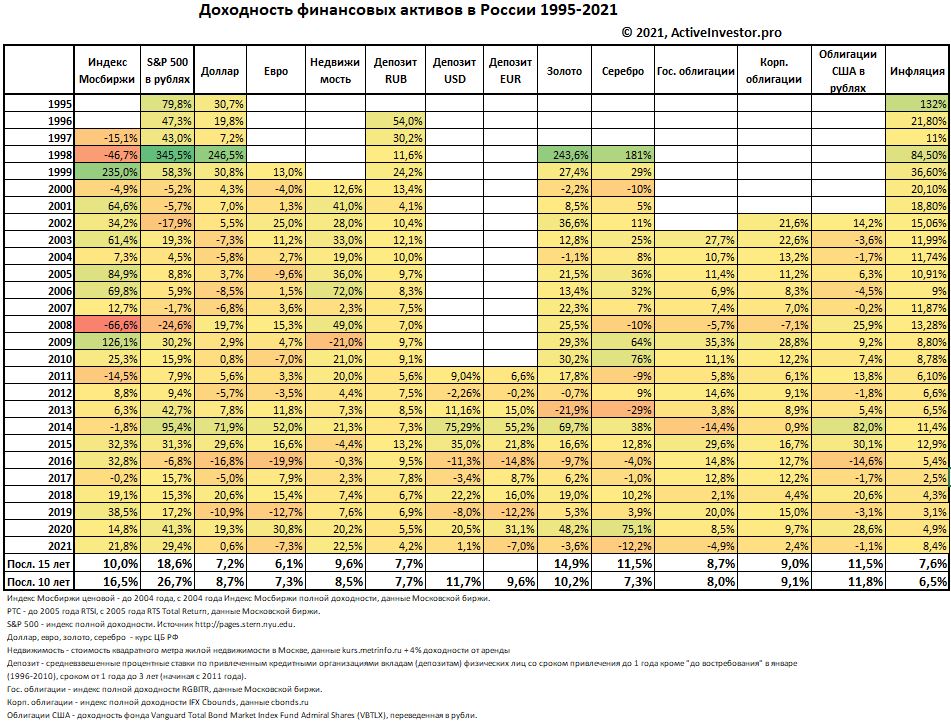
Те, кто давно читает мой блог, знают, что я регулярно веду таблицу с доходностью основных финансовых активов. В ней отражена доходность с начала по конец года основных финансовых активов — акций, облигаций, недвижимости, валюты, вкладов. Так же посчитана доходность американских акций и облигаций, переведенная в рубли, для сопоставления с доходностью рублевых активов.
В последние несколько лет иностранные активы становятся российскому инвестору все ближе и ближе. Все началось с появления биржевых фондов ETF Finex, которые были первыми биржевыми фондами, давшими возможность инвестирования в иностранные индексы на Московской бирже. С годами ассортимент биржевых фондов увеличивался, появились российские биржевые ПИФы, иностранные акции. Сегодня на бирже торгуется несколько десятков биржевых фондов на различные российские и иностранные активы. И с годами их число будет скорее всего только увеличиваться, предоставляя российскому инвестору все больше возможностей для диверсификации и разнообразия своего инвестиционного портфеля.
Поэтому было бы интересно найти некий «идеальный» портфель для российского инвестора (почему слово идеальный заключено в кавычки, вы узнаете позднее) с оптимальным сочетанием различных активов. Про принципы составления инвестиционного портфеля я здесь подробно рассказывать не буду, так как для этого есть целая серия статей про Asset Allocation. Цель будет составить портфель из различных классов активов, и найти их пропорции для составления портфеля с наилучшим соотношением риска и доходности.
Выбор активов
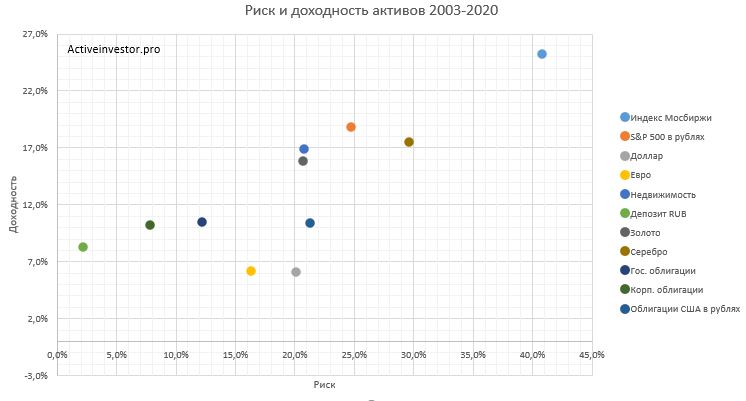
Портфель будем составлять по пассивной стратегии, то есть из индексов. Для начала посмотрим на исторический риск и доходность финансовых активов. По горизонтальной оси отложен риск (стандартное отклонение). По вертикальной — среднегодовая доходность актива. Как видим, самая большая доходность у индекса Московской биржи 25,2%, но и риск самый высокий 39,7%.
Ниже по доходности идет индекс S&P 500: доходность 18,8%, риск 24,1%. Дальше по доходности идет серебро 17,5% при риске 28,8% — у него доходность чуть меньше, но риск больше по сравнению с S&P 500.
Недвижимость и золото располагаются рядом друг с другом, то есть имеют примерно равную доходность 15-16% и риск 20-21%. Ниже по доходности располагаются облигации США и РФ — возврат около 10%. Но по риску они сильно различаются — гособлигации РФ имеют риск 11,9%, а облигации США 20,7%. Это связано в первую очередь с тем, что на доходность облигаций США (как и любых других активов, номинированных в долларах) сильное влияние оказывает колебание курса рубля, которое порой достигало пары десятков процентов в год.
Средняя доходность корпоративных облигаций РФ еще ниже — 10,2% при риске 7,6%. Вклады в банках в среднем приносили 8,2% при стандартном отклонении доходности 2,2%. Самые низкодоходные активы — это валюта — наличный доллар и евро. Доходность 6% при риске 16% и 19% соответственно.
Что включать в портфель?
Хоть таблица и содержит много различных активов, нет смысла брать в портфель все. В портфель нужно включать активы, которые:
- приносят положительную реальную доходность;
- не связаны между собой или говоря математическим языком, имеют низкую положительную, а еще лучше нулевую и даже отрицательную корреляцию между собой;
- ими легко управлять.
Есть смысл исключить валюту и вклады, как наименее доходные инструменты. Банковские вклады убираем, на бирже они не торгуются, и вместо них есть облигации. Недвижимость тоже проблематично купить на бирже, разве что только через закрытые ПИФы недвижимости, но они малоликвидны и имеют большой порог входа. Поэтому для включения в портфель оставим акции РФ и США, облигации РФ и США и золото.
В итоге мы получим портфель, в котором будет три класса активов — акции, облигации, товары. Портфель будет диверсифицирован по двум странам и по степени их развития, одна из которых развитая, другая — развивающаяся.
Взаимосвязь активов друг с другом
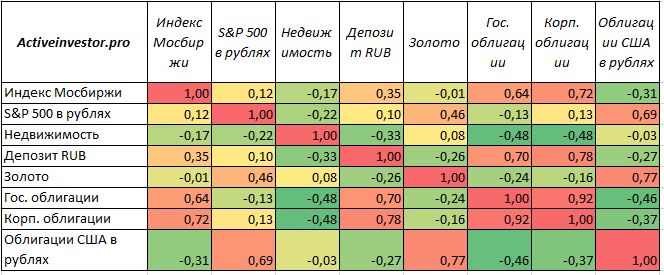
Посмотрим на матрицу корреляции активов. Говоря простым языком, корреляция показывает, насколько связаны между собой движения двух активов. Корреляция может принимать значения от -1 до +1.
+1 означает, что активы движутся абсолютно одинаково, 0 — что между ними нет взаимосвязи, -1 — активы движутся противоположно друг другу. Отрицательная корреляция для нас самый лучший вариант. Как видно, среди некоторых выбранных активов есть отрицательная корреляция.
Самая низкая корреляция у недвижимости и российских облигаций. Так же отрицательная корреляция наблюдается у акций РФ с облигациями США и недвижимостью. Нулевая корреляция у акций РФ с золотом и S&P 500. У золота отрицательная корреляция с российскими облигациями. У российских облигаций отрицательная корреляция к облигациям США.
Наличие в портфеле активов с низкой корреляцией будет снижать общий риск портфеля. В то время, когда одни актив будут падать, другие будут дорожать или не падать. Потом они могут поменяться местами и т.д. Таким образом общая динамика портфеля будет сглаживаться.
Расчеты
Итак, все вводные данные у нас есть: историческая доходность, корреляция, активы для включения в портфель выбраны. Теперь нужно приступить к расчетам. Дальше с помощью Excel мы составим несколько десятков тысяч портфелей, посчитаем их среднюю доходность и риск, и выберем наилучшие по соотношению риск/доходность. Для этого нам понадобится составить так называемую границу эффективности портфелей по Марковицу (Efficient Frontier).
Сначала посчитаем среднюю доходность каждого актива. Это будет наша ожидаемая доходность от актива. Заодно посчитаем Дисперсию, Стандартное отклонение (Риск).
И еще посчитаем соотношение доходности и стандартного отклонения — чем больше это значение, тем больше доходность и меньше риск. Будем считать, что это упрощенный коэффициент Шарпа (хотя настоящий Шарп учитывает доходность безрискового актива, а мы нет), который показывает, насколько хорошо доходность компенсирует принимаемый риск.
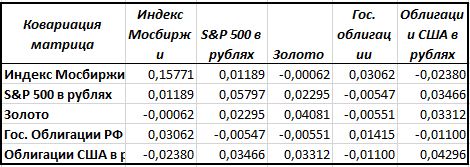
Следующий шаг — построить матрицу ковариации между активами. Ковариация математически показывает, как два актива зависят друг от друга. Чем больше число, тем больше зависимость между ними, и наоборот. Эта матрица потребуется нам для дальнейших вычислений.
Расчет доходности портфеля
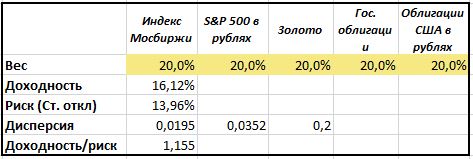
Построим табличку, которая вычислит доходность и риск портфеля с определенными долями активов. В первой строке зададим веса активам — по 20% каждый.
Во второй строчке посчитаем доходность такого соотношения активов — она равна сумме произведений средней доходности актива на его долю в портфеле.
В третьей строчке посчитаем стандартное отклонение портфеля — оно равняется квадратному корню из дисперсии, которую мы считаем в четвертой строчке. Дисперсия — это сумма произведений матрицы ковариации и долей активов в портфеле.
И в последней строчке рассчитаем соотношение доходности и риска.
У нас получилось, что равновзвешенный портфель имеет доходность 16,12%, риск 13,96% и коэффициент Шарпа 1,15.
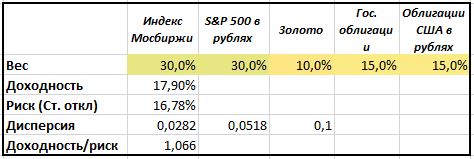
Теперь поменяем доли активов в портфеле. Увеличим долю акций до 60% и уменьшим долю остальных активов: золото пусть занимает 10%, а облигации по 15%. Получим следующий результат: Доходность выросла до 17,9%, Риск до 16,78%, Шарп снизился до 1,06. Такой портфель, хоть и приносит больше доходности, но и риск тоже увеличивается. Причем риск увеличился больше, чем доходность, о чем нам говорит снизившийся коэффициент Шарпа.
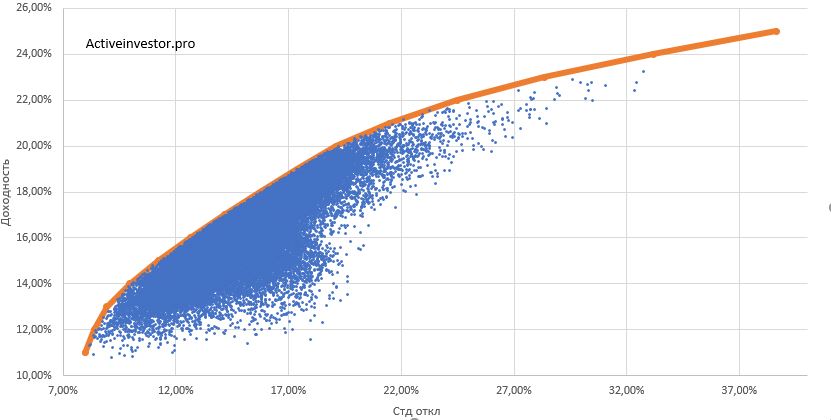
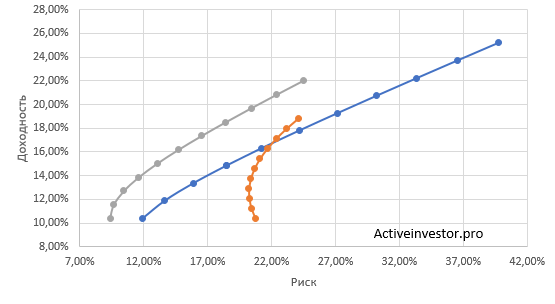
Теперь пойдем дальше. С помощью магии Excel сделаем расчеты доходности и риска для нескольких десятков тысяч портфелей с самыми разными пропорциями активов. Полученные результаты я свел в диаграмму. На ней мы видим огромное множество точек. Каждая точка — это портфель с какими-то пропорциями активов. По горизонтальной оси отложен риск (стандартное отклонение портфеля), по вертикальной — его доходность.
Оранжевым выделена граница эффективности портфелей. Это линия, на которой расположены портфели с наименьшим уровнем риска. Это именно та линия, на которой стоит искать оптимальный портфель.
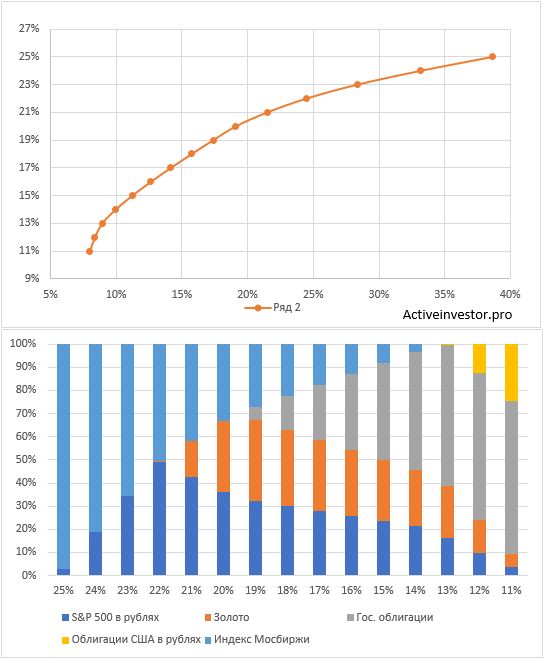
Находим идеальный портфель инвестора
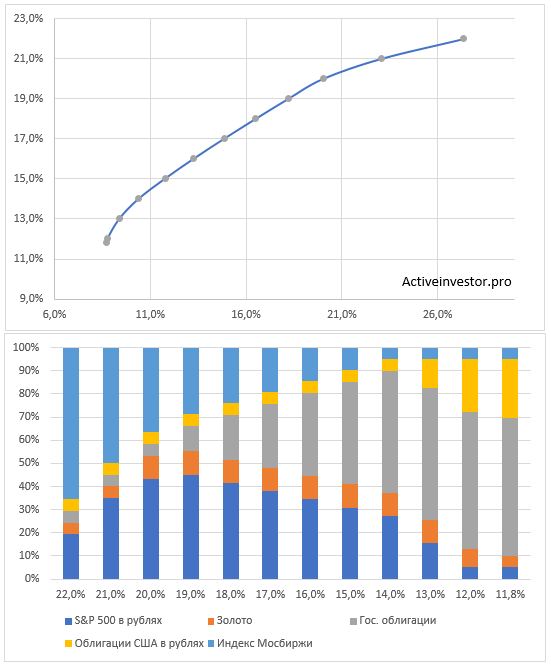
На графике ниже я убрал все лишние портфели и оставил только те, что лежат на границе эффективности. На ней отложены портфели с доходностью от 25% до 11% и наименьшим риском. Так же с помощью диаграммы я отобразил пропорции активов в каждом портфеле в зависимости от доходности.
Портфель, имеющий наибольший коэффициент Шарпа 1,46 получился со следующим составом:
- Акции РФ 0%
- Акции США 16%
- Золото 23%
- Облигации РФ 61%
- Облигации США 0%
Очевидно, состав получился неоднозначным. В нем нет акций РФ, облигаций США, зато большая доля облигаций РФ и золота. Но это неудивительно. Если мы посмотрим на таблицу с вводными данными, именно у этих двух активов исторически было наилучшее соотношение доходности и риска. Поэтому портфель получился именно таким. Очевидно, что он является несбалансированным и вряд ли в него вряд ли стоит инвестировать. Исторические данные играют с нами злую шутку.
Попробуем с этим что-то сделать. Внесем ограничение, что доля актива в портфеле не может быть меньше 5%. А для золота дополнительно установим еще и верхнюю границу в 10%.
В результате мы получим портфель с наилучшим коэффициентом Шарпа 1,38 и следующим составом:
- Акции РФ 5%
- Акции США 16%
- Золото 10%
- Облигации РФ 57%
- Облигации США 13%
Портфель снова получился весьма консервативным с долей облигаций в 70%. Но это нормально. Например, для портфеля, состоящего только из американских акций и облигаций, наилучший коэффициент Шарпа исторически находится в составе 85% облигаций и 15% акций.
Для увеличения доходности нужно увеличивать риск, а Шарп при этом будет снижаться. Например, если мы хотим получить портфель с доходностью 15% годовых, то состав портфеля был таким:
- Акции РФ 10%
- Акции США 31%
- Золото 10%
- Облигации РФ 44%
- Облигации США 5%
Если нужна вожделенная доходность в 20%, то состав портфеля был таким:
- Акции РФ 37%
- Акции США 43%
- Золото 10%
- Облигации РФ 5%
- Облигации США 5%
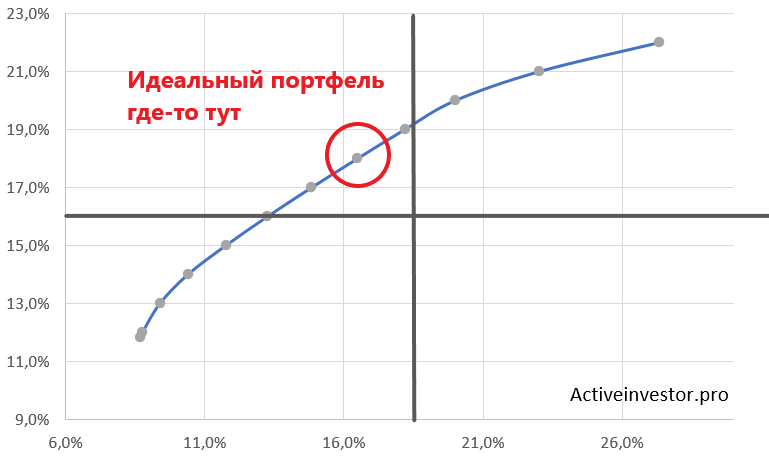
Как выглядит идеальный инвестиционный портфель?
Если мы поделим график с множеством портфелей на квадраты, то идеальный портфель будет находиться в левом верхнем квадрате. Потому что именно там будут располагаться портфели с наибольшей доходностью и наименьшим риском.
Я выделил на линии область, где должен располагаться оптимальный портфель. Если посмотреть на пропорции активов в таком портфеле, то они будут такими:
- Акции РФ 24%
- Акции США 42%
- Облигации РФ 19%
- Облигации США 5%
- Золото 10%
или такими:
- Акции РФ 19%
- Акции США 38%
- Облигации РФ 28%
- Облигации США 5%
- Золото 10%
Выводы
Выводов можно сделать много. В каком месте на границе эффективности искать свой «идеальный» портфель каждый решает сам в зависимости от своих ожиданий по риску и доходности. Но можно выделить несколько интересных моментов.
Сперва нужно сделать предупреждение — полученные результаты основаны на исторической доходности активов с 2003 года, то есть включают 19 лет. Это уже не мало, но и не так много. Например, статистика рынка США насчитывает десятки лет. А значит наши результаты могут иметь некоторые искажения в силу небольшого срока. Ну и всем известная мантра: доходность в прошлом не гарантирует доходности в будущем.
Наш портфель составлен из трех классов активов — акций, облигаций и товаров. А так же диверсифицирован по двум странам, имеющим разную степень развития и экономику. За эти два десятилетия РФ и США пережили разные циклы. РФ бурно росла в первое десятилетие благодаря ценам на нефть, это было десятилетие развивающихся рынков. Для США это десятилетие было тяжелым — сначала кризис доткомов в 2000, спустя 8 лет ипотечный кризис. Зато после 2010 все поменялось — рынок США начали бурный рост, а экономика РФ впала в стагнацию, как и остановившиеся в росте цены на нефть. Благодаря наличию двух стран в портфеле они балансировали друг друга.
Золото было очень эффективным вложением. Оно принесло высокую доходность на этом отрезке времени и имело негативную корреляцию с российскими активами. Поэтому Excel так настойчиво добавлял большую долю золота в портфель. Золото сильно росло в первое десятилетие 21 века. Но второе десятилетие цены на золото не росли такими темпами. В долларах золото в реальном выражении даже снизилось. В России его доходность осталась высока в первую очередь благодаря ослабевшему в более чем два раза курсу рубля. Поэтому делать в будущем большую ставку на золото я бы не стал.
Акции РФ и США имели очень хорошую доходность и низкую корреляцию. Поэтому их сочетание в портфеле принесло свои плоды. Причем результат показывает, что доля акций США должна была быть чуть больше, чем доля РФ. Оптимальное соотношение между ними 60/40.
Облигации РФ безусловно являются самым стабильным из всех активов и выполняют основную роль для снижения риска. Облигации США при такой же средней доходности имели риск в два раза больше. Но их корреляция с облигациями РФ сильно отрицательная. Поэтому было целесообразно добавлять в портфель лишь небольшую часть американских облигаций. Оптимальное соотношение между облигациями РФ и США 70/30 или 80/20.
Все полученные портфели смогли обогнать инфляцию, которая на выбранном отрезке составляла в среднем 8,3%.
Предвосхищая вопрос, а может быть стоило составить портфель только из американских или только из российских активов? Отвечу — нет. Международные портфели (серый график) заметно выигрывают по риску и доходности у моно-национальных портфелей (синий и оранжевый). Рекомендую прочитать: Зарубежные активы в портфеле российского инвестора
Мы нашли «идеальный» портфель для прошлого. Останется ли он идеальным в будущем, покажет только время. Я не рекомендую всем в него инвестировать. Но он может послужить хорошей основой для составления своего инвестиционного портфеля.
Если тенденции прошлого будут продолжаться и в будущем, то эти расчеты помогут вам найти свой инвестиционный портфель, «путешествуя» по границе эффективности. А постепенно идущее расширение ассортимента биржевых индексных фондов дает новые возможности по включению в портфель других классов активов, делая портфель еще более диверсифицированным и разнообразным.




Интересно конечно. Но, если честно то нифига не понятно!
Возможно, если вы ранее не читали про стратегию распределения активов Asset Allocation, то здесь вам будет не все понятно 🙂
Я не стал детально описывать все в одной статье, иначе она бы разрослась до неприличных размеров. Поэтому рекомендую почитать про это отдельно https://activeinvestor.pro/tag/asset-allocation/
идеально-)
По большому счету для большинства: физики-домохозяйки 🙂 тех ко не хочет разбираться, но хочет доходность, подойдут инвестиции в индексы. Покупать постоянно, раз в месяц, квартал, год и т.п. Чутка держать в облигациях на случай просадок, чтобы был кэш для закупки дешевле. Собственно, все, больше ничего не нужно.
p.S. для wp есть крутой плагин для комментов wpDiscuz, рекомендую
В общем да, чем проще стратегия, тем лучше)
Это очень интересная статья, но если считать шарпы и доходности корректно, то есть за вычетом безрисковой доходности, то результаты получатся совершенно другими, мне бы было интересно взглянуть на результаты именно по такой методологии.
Спасибо. Что значит, результаты получатся совершенно другими? Можете привести пример?
Суть следующая. Когда вы считаете шарп на номинальных доходностях, вы завышаете ценность облигаций, из-за этого вам пришлось их «выгонять» насильно.
Причина следующая, облигации вроде как дают лучший шарп, потому что их доходность примерна равна СКО, а у акций в 2 раза ниже (по вашим данным)
Но Шарп придумал шарп не для того, чтобы просто сопоставить СКО со средней доходностью, безрисковая доходность появилась не просто так, а чтобы понять, насколько имеет смысл рисковать.
То есть допустим доходность безрискового вложения 7%, облигации 10% (СКО 10%), а акций 20% (СКО 40%).
На деле у нас есть гарантированные 7%, поэтому нам надо оценить премию за риск.
И тогда получится не так радужно.
У облигаций премия за риск 3%, а у акций 13%. СКО при этом не меняется практически
И получается 3/10 против 13/40, частные почти равны, получаем, что в акциях не так уж глупо рисковать.
Я убежден, что без премии за риск коэффициент Шарпа малоинформативен и даже вводит в заблуждения, потому что он базируется на понятии премии за риск.
Да, понятно, спасибо за пояснения. Конечно, так считать было бы правильнее, но мне было немного лень. Все же думаю, статья от этого не сильно потеряла.
Очень жаль, что лень, результаты мне лично прям очень интересны были бы.
Может когда-нибудь через годик надумаете.
Интересная статья. Жалко конечно что snp с крахом доткомов не влез, было бы интересно посмотреть портфель и на доходность с потерянными 13 годами, а так получается не очень объективно по отношению к ммвб по доходности. Так как в ммвб как раз в этот период влезло много плохих или средних доходностей.